https://atcoder.jp/contests/abc146/submissions/12441749
青dif問題は天才解法すぎる…
要素の和・余りということで、とりあえず累積和のMODを取ってみる。
MOD([R, L]の総和) = MOD(累積和R - 累積和L) = MOD(indexR - indexL) が成立すれば良い(indexR - indexL < K なのでindexもMODを取っておく)わけだが、成り立つかどうか全てのRとLを単純に全探索するとになってしまう。
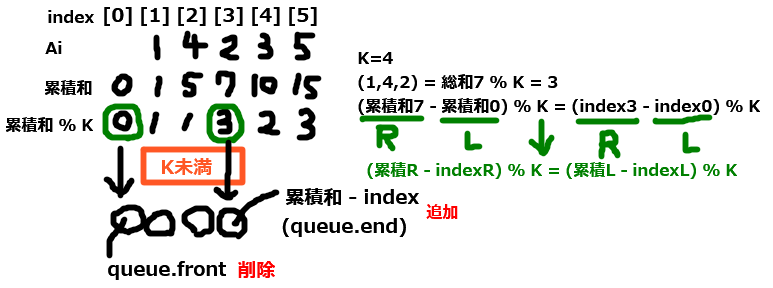
ここで、Rを決め打ちするような式変形をする。即ち (累積和R - indexR) % K = (累積和L - indexL) % Kとする。mapとqueueを使うと左辺と一致する右辺の個数がで取得できる。具体的には決め打ちするRを0からNまでインクリメントしながらmapとqueueに(累積和 - index)の値を追加していく。全体計算量は
になる。
- map[累積和[i] - index]++; (累積和[i] - index)となる値の個数をインクリメント
- ans += map[累積和[i] - index]; (累積和[i] - index)と同値な個数を答えに加算
- if (K <= queue.size()) キューの範囲がKを超えるかどうか調べる
- map[queue.front()]--; キューの先頭の(累積和[i] - index)となる値の個数をデクリメント
連続部分列のオーダーを下げるテクニック→Rを決め打ちした式変形およびmapとqueueを使った高速化
このあたりを暗記するのが良さそうな感じがする