ダイクストラ法
単一始点から全ての終点までの最短経路を求める
ダイクストラの経路は木になる(最短経路木)
https://snuke.hatenablog.com/entry/2021/02/22/102734
ダイクストラの処理は一次元DPの応用と認識することが出来る
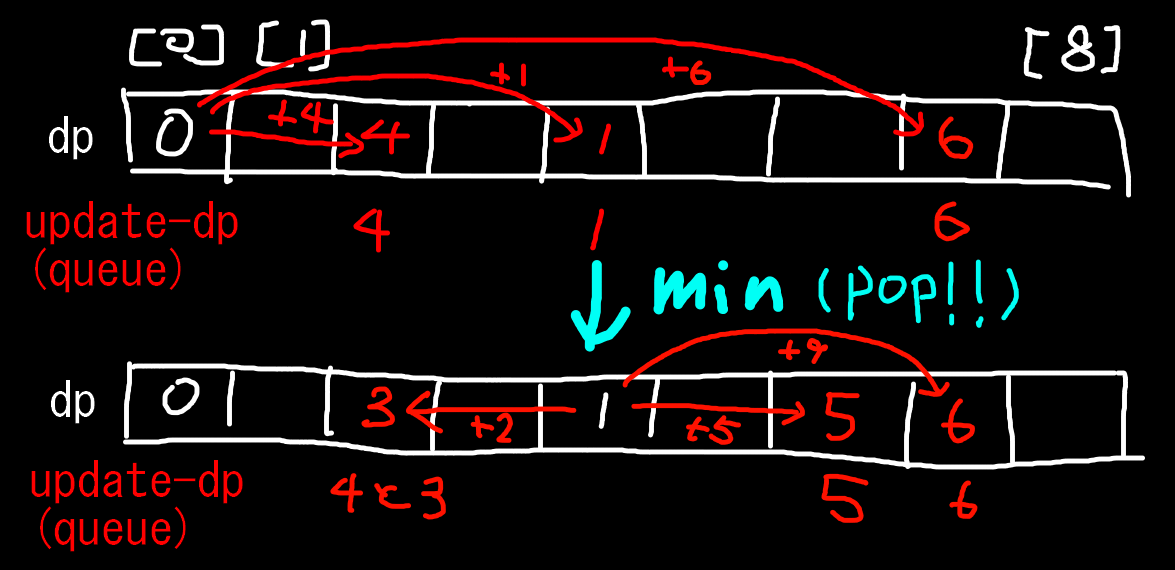
計算量は 
- 計算量は天才でないと理解できない(要出典)
- 全頂点の次数合計が2Eなのでキューの更新回数が
(鉄則本)
- https://www.akiradeveloper.com/post/dijkstra-analysis/
- kステップ時の漸化式は dp[i] = k-1ステップ時での最善集合から遷移できる集合のうちの最善 と認識することもできそう
- キューからPOPした頂点⇔最善が確定した頂点 POPした頂点が暫定で後から更新されるグラフは作成不能な気がしてきたのでキュー追加は
auto dijkstra
#include <bits/stdc++.h> using namespace std; using ll = long long; using vl = vector<ll>; auto dijkstra = [&](wgraph& g, ll s, ll INF) -> vl { vl res(g.size(), INF); priority_queue<pll, std::vector<pll>, std::greater<pll>> pq; res[s] = 0, pq.push({ 0, s }); // スタート地点の最短距離はゼロ while (!pq.empty()) { auto [val, now] = pq.top(); pq.pop(); if (res[now] != val) continue; for (auto& [next, cost] : g[now]) { if (res[now]+cost < res[next]) { res[next] = res[now]+cost; pq.push({ res[next], next }); } } } return res; };
LIB::Dijkstra
- DijkstraResult Run(wgraph& g, ll s, ll inf, ll mod = 998244353)
重み付きグラフ g に対して頂点 s から全ての終点までの最短経路を求める(到達できない頂点は inf を返す)
戻り値 DijkstraResult について
min_cost[i]: パス s->i 最短経路コスト
pass_count[i]: パス s->i 最短経路数
prev_vtx[i]: 頂点 i->v 遷移 prev_vtx[i] = v
GetPath(s, t): s-t 最短経路を復元、復元不能なら空のvectorを返す
#include <bits/stdc++.h> namespace LIB { struct DijkstraResult { using ll = long long; std::vector<ll> min_cost; std::vector<ll> pass_count; std::vector<ll> prev_vtx; DijkstraResult(ll n, ll s, ll inf) { // n = 頂点数, s = スタート地点, inf = 到達不可能 min_cost.resize(n, inf); min_cost[s] = 0; pass_count.resize(n, 0); pass_count[s] = 1; prev_vtx.resize(n, -1); } std::vector<ll> GetPath(ll s, ll t) { std::vector<ll> path; for (ll v = t; v != -1 && v != s; v = prev_vtx[v]) { path.push_back(v); if (prev_vtx[v] == -1) path.clear(); if (prev_vtx[v] == s) path.push_back(s); } std::reverse(path.begin(), path.end()); return path; } }; struct Dijkstra { using ll = long long; using pll = std::pair<ll, ll>; using wgraph = std::vector<std::vector<pll>>; DijkstraResult Run(wgraph& g, ll s, ll inf, ll mod = 998244353) { DijkstraResult res(ll(g.size()), s, inf); std::priority_queue<pll, std::vector<pll>, std::greater<pll>> pq; pq.push({ 0, s }); while (!pq.empty()) { auto [value, now] = pq.top(); pq.pop(); if (res.min_cost[now] < value) continue; for (auto [next, cost] : g[now]) { PrevPath(now, next, cost, res); PassCount(now, next, cost, mod, res); if (res.min_cost[now] + cost < res.min_cost[next]) { res.min_cost[next] = res.min_cost[now] + cost; res.prev_vtx[next] = now; pq.push({ res.min_cost[next], next }); } } } return res; } private: void PrevPath(ll now, ll next, ll cost, DijkstraResult& res) { // 最短経路復元で使う経路遷移元を更新 if (res.min_cost[now] + cost < res.min_cost[next]) res.prev_vtx[next] = now; } void PassCount(ll now, ll next, ll acost, ll mod, DijkstraResult& res) { // 最短経路数を更新 if (res.min_cost[now] + acost < res.min_cost[next]) res.pass_count[next] = res.pass_count[now]; else if (res.min_cost[now] + acost == res.min_cost[next]) res.pass_count[next] += res.pass_count[now]; res.pass_count[next] %= mod; } }; }